こんにちは。
今回は、サイコロを使いながら 隠れマルコフモデル(Hidden Markov Model) をテーマにしたいと思います。
隠れマルコフモデルはDNA解析や、音声解析で利用されている基礎テクニックです。
ベイズ統計「見えないものをさぐる ―それがベイズ」を出版しました。詳しくはこちらをご覧下さい。
画像認識と強化学習(DQN)を中心とした、ディープラーニングの書籍「実装 ディープラーニング」をオーム社から出版しました。詳しくはこちらをご覧下さい。
サイコロゲーム
サイコロは、みなさん良くご存じのとおり、1~6 までの目があって、その目の出方(確率)は、どの目をみても「同様に確からしい」というものです。
今回は少し物語風です。
AさんとBさんは、Cさんの家で 3 人でサイコロゲームを行いました。
ゲームはいたって簡単で、それぞれが見えないように数字を紙に書いて、 1 個のサイコロを振って、紙の数字とサイコロの目があっていれば勝ちというものです。
サイコロを振るのはCさんで、Cさんがいわゆる胴元です。
Aさんは、あとでサイコロの目を確認したかったので、出た目をすべて記録していました。
サイコロは全部で 200 回投げられましたが、中盤あたりからCさんの勝ちが目立つようになり、最後はCさんの一人勝ちになりました。
負けたAさんは、悔しいというより、何か違和感を感じました。
そこでAさんは、家に帰ったあと、サイコロの出た目を一覧にしてみました。
|
<サイコロの出た目の一覧(200個)> 12442552156235244611513665441521334522422516131461324351224626256625324354313241416144163515363423135135313531535155116446122436632362242642626642654256461421553232365354361461451264546335353161532646 |
うーん、これでは全くわかりません。
そこでサイコロの、 1~6 の目が何回出たのかを整理してみました。

1~6 の目の出方はきれいにばらついていて、サイコロに不正があるようには思えません。
また統計的にサイコロの 適合度検定 (自由度 5 、0.05 )をしても、偏りがあるとは言えないようです(下記参照)。
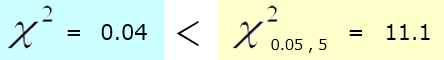
悲しいかな、Aさんの追及はここまででした。
あとは、自分は運が悪かったと考えるしかありません。
隠れマルコフモデル
一方、Bさんも目の出方に少し違和感を感じていました。
Bさんは、途中でCさんがサイコロをすり替えて目の出方を変えながら、最終的に不自然にならないように調整したのではないか? と考えました。
そこでBさんは、Aさんからサイコロの出た目の一覧を借りて、 隠れマルコフモデル(Hidden Markov Model) を利用し、この200個のサイコロの目の中で、目の出方の分布が変わったところをあぶり出したいと思いました。もしサイコロをすり替えたのであれば、途中でサイコロの目の出方の分布が変わっているはずです。
サイコロの目の出方の分布の遷移を調べるのは、隠れマルコフモデルが有効だと考えました。
分布を探し出すには バウム・ウェルチアルゴリズム(Baum-Welch algorithm) という方法を使います。
これは、バウムさん、ウェルチさんという人が考え出したアルゴリズムです。
サイコロの目の 200 個の結果の中に、分布の偏りがあると仮定して「バウム・ウェルチアルゴリズム」を使って分布を探してみました。
するとなんと!異なる2種類の分布があることがわかったのです!
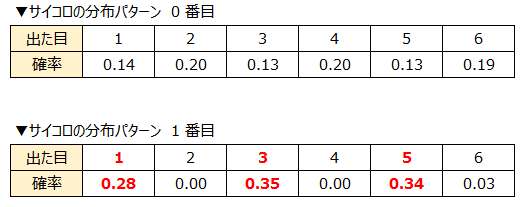
サイコロの分布パターン 1 番目は、この 200 個の中で 奇数の目が連続で出ている ところがあることを示しています!
たかだか200個の数字なので、目で追って「奇数の目が連続しているところ」を探すこともできますが、 ビタビアルゴリズム(Viterbi algorithm) という方法を使うと、効率的に「奇数の目が連続しているところ」を探すことができます。
これは、ビタビさんという人が考え出したアルゴリズムです。
2つの分布があることを前提にこのアルゴリズムを利用すると、以下のような結果になりました。
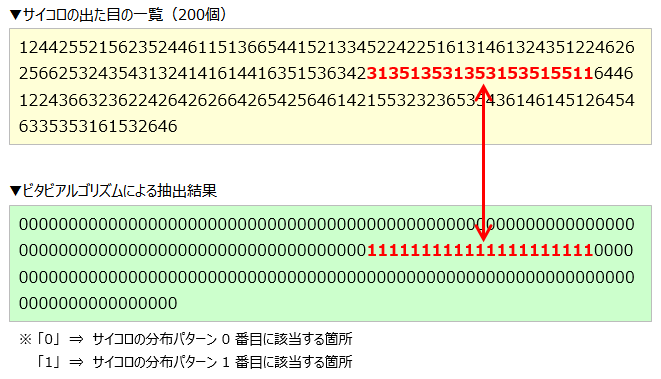
ついにシッポを見つけました!
1 が連続しているところ、すなわち 98 回目から、 118 回目までの 21 回が連続で「奇数」になっています。
「奇数が連続 21 回出る」のは通常ありえそうなことでしょうか?
奇数、偶数が出る確率を 0.5 として二項分布で考えると、奇数が 21 回連続する可能性はなんと 0.000048 % です。
これはやはりサイコロを変えたとしか考えられません。奇数が出ると予めわかっている状態で、紙に奇数を書けばあたる確率は大きくなります。
さて、 200 回トータルでは出た目のつじつまが合っているのですから、連続する奇数があるということは、どこかに連続した偶数も隠れているに違いありません。あるいは、低めの数が出やすいサイコロ、高めの数が出やすいサイコロなどにすり替えた可能性もあります。
そこでBさんは、次の 5 パターンの分布をもったサイコロを考えました。
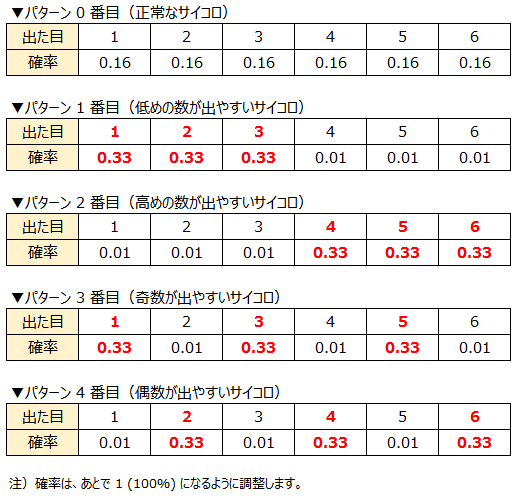
この 5 つの分布パターンから、「ビタビアルゴリズム」を利用してそれぞれのパターンを探すと以下のようになりました。
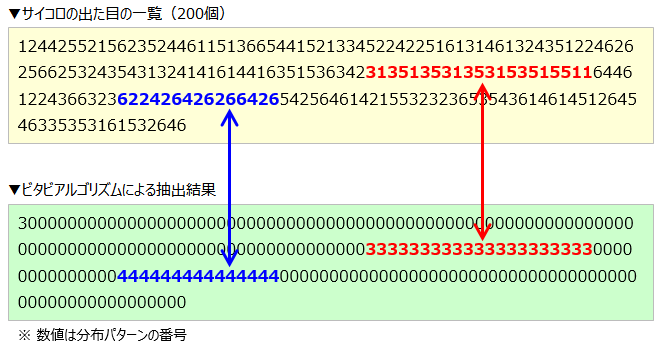
0 は正常なサイコロ、 3 は奇数が出やすいサイコロ、 4 は偶数が出やすいサイコロです。
この結果から、Cさんは最初は正常なサイコロを使って、途中から奇数が出やすいサイコロにすり替え、さらにあとで偶数が出やすいサイコロにすり替え、最後はまた正常なサイコロに戻したことがわかります。
これでCさんの不正が明らかになりました!!!
200個くらいのサイコロデータであれば、なんとか目で追って、「おや?」という所を探すこともできますが、これが万単位の個数になってくると、とても目で追おうという気にはなれません。
そんなときは、この「隠れマルコフモデル」を使って解析を進めることがとても有効な手段になりそうです。
ここで今回のサイコロの出た目を、下記のように英字に置き換えてみます。
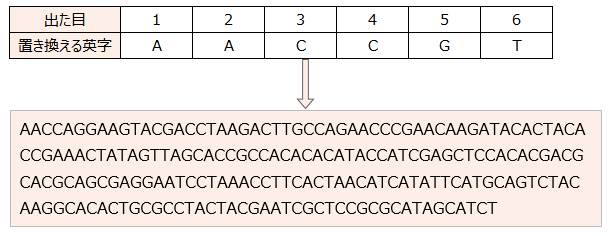
これはDNAのデータに似てますね。
DNA解析ではこのようなデータが数千万行あって、そこからひたすらバウム・ウェルチアルゴリズムやビタビアルゴリズムなどを使って、分布パターンを探しています。
バウムさん、ウェルチさん、ビタビさんの業績は大きいですね。
サイコロの結果を音声データと考えれば、 音声解析 にも利用できそうです(実際、利用されているようです)。
サイコロの出た目は実際に人が観測できるデータです。これに対し、「奇数が出やすいサイコロ」は普通は直接観測できない内部の状態です。この隠れた内部を明らかにしようというのが “隠れ” マルコフモデルで、「内部の状態によって表の観測できるデータが決まる」 という考え方です。
内部の状態を探るという意味では、 因子分析 に似ているようです。
