強化学習でボールを自由に動かす　～ネズミを追いかけるボール～　Part 1

DQN　（Deep Q Learning）
DDQN　（Double DQN）
DDPG　（Deep Deterministic Policy Gradient）
NAF　　（Continuous DQN （CDQN ））
CEM　　（Cross-Entropy Method）
Dueling DQN　（Dueling network DQN）
Deep SARSA
A3C　　（Asynchronous Advantage Actor-Critic）
PPO　　（Proximal Policy Optimization）

１　Q学習（DQN）

DQN はDeep Learningを用いた強化学習の一つですが、ベースとなっているアルゴリズムはQ学習（Q-Learning）です。このQ学習を「蟻」を主人公にして説明します。

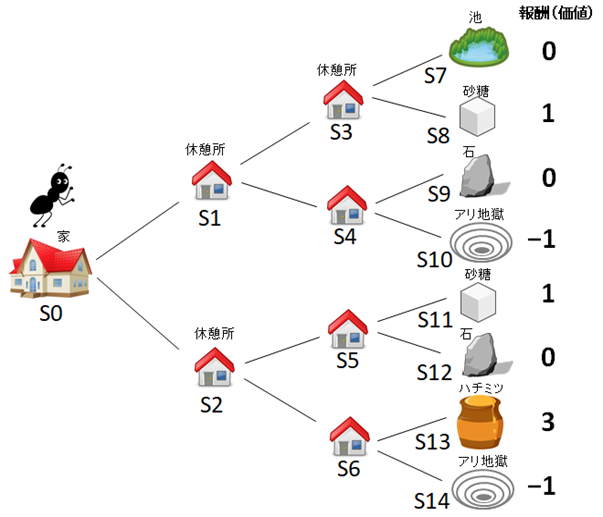
図１

（１）学習時の蟻の行動

　図１は、蟻がこれから餌をとりにいく様子を表しています。途中に休憩所があり、最後に餌があります。餌にはそれぞれ得点がついています。大好きなハチミツであれば３点、砂糖は１点です。しかし間違って「アリ地獄」にはまる場合もあり、その場合は－１点としています。この得点は「報酬」と呼ばれています。

　蟻はそれぞれの休憩所の掲示板に得点を書き込んでいきます。そのとき、蟻の行動には次のような２つのルールがあります。

　①蟻は次のポイントの状態（だけ）を見渡せる

　②次のポイントの得点（報酬）の中で一番いい得点を、今いるポイントの掲示板に書きこむ

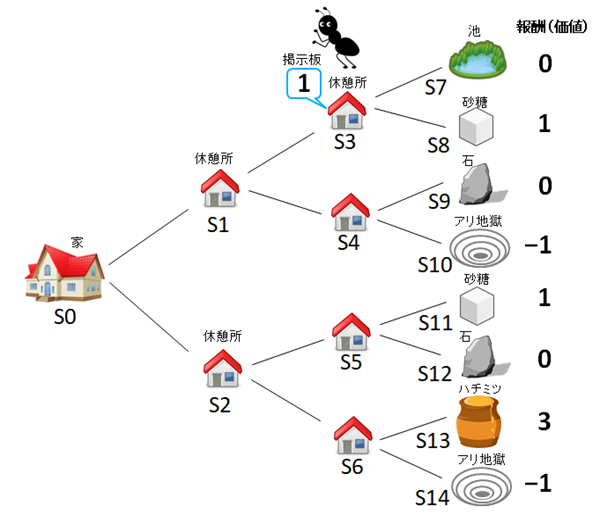
図２

　さて、いよいよ学習スタートです。図３のように、はじめに蟻が休憩所S1に進んだとしましょう。この時、蟻は次のポイントS3とS4を見渡しますが、まだ掲示板がないので、S1の掲示板には「0」と書くことにします。さらに蟻が休憩所S3まで進んだとすると、見渡すとS7の報酬には0、S8には報酬1があるので、S3の掲示板には（良い報酬の）「1」を書きこみます（図４）。

図３

図４

　この蟻が、再び家から出発して、同じようにS1　→　S3　と進むと、掲示板の情報は図５のようになります。最後のポイントには砂糖がある、すなわち報酬として最後に「１」があるという情報が、次第に家のほうにたぐり寄せられていくことがわかります。　

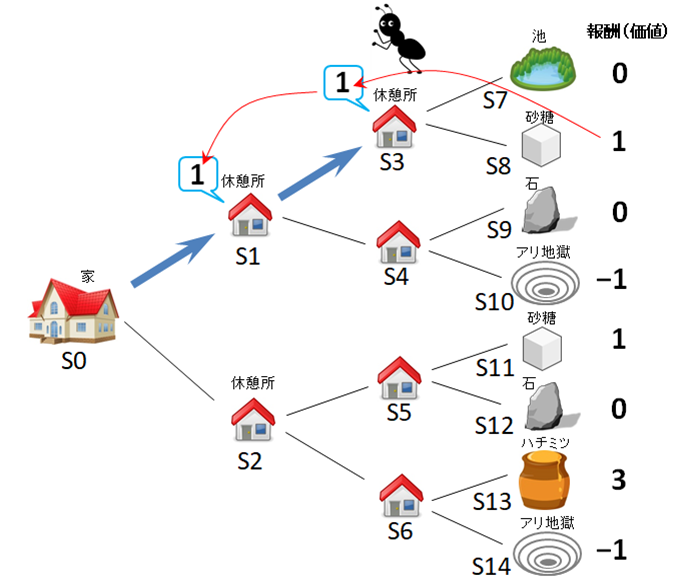
図５

　蟻が適当に（ランダムに）休憩所を選択し、何回も餌を探しにいくと、掲示板の情報は最終的に図６のようになります。すべての休憩所の掲示板に得点（Q値）が書いてありますので、次に餌を探すときは、もう迷いません。これで蟻の学習はひとまず終了です。

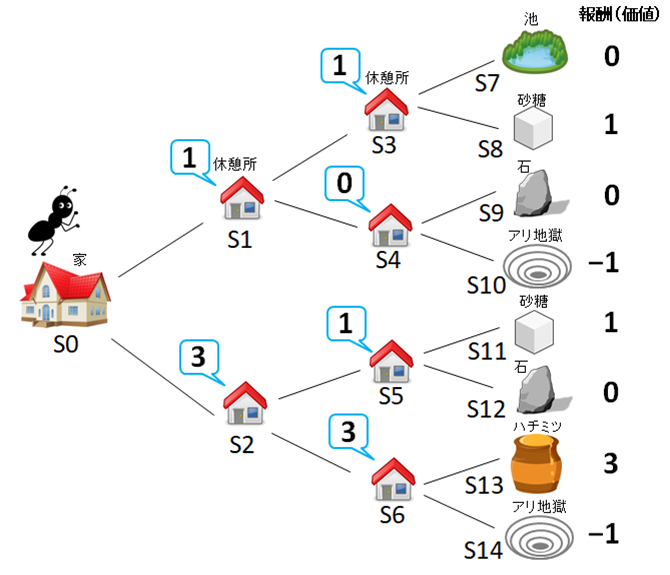
図６

（２）推測時の蟻の行動

　学習が終わったので、次はこの掲示板の得点を使った、最もよい餌の見つけ方を考えていきます。
見つけ方のルールは次の２つです。

　①蟻は、今来た道順を覚えていない

　②一番大きな得点が書いてある休憩所を選ぶ

　このような学習・推測方法はQ学習と呼ばれています。このQ学習にディープラーニングの手法を加えたものがDQNです。

２　決定論的と確率論的

　図６では、働き者の蟻のおかげで、立派な掲示板を作ることができました。キリギリスではこうはいきません。おそらく砂糖を見つけたあたりで、掲示板の作成をやめてしまうでしょうね。

　蟻は、「一番大きな得点が書いてある掲示板を選ぶ」というルールに従ってさえいれば、必ず、毎回「ハチミツ」を得ることができます。

　しかし、（おそらく蟻もそうだと思いますが）毎日毎日、朝、昼、晩にハチミツを食べ続けるのは、さすがに飽きてきますよね。たまには砂糖をなめたいとか、池の水を飲みたいという気持ちもでてくると思います。せっかく立派な掲示板を作っても、「一番大きな得点がかいてある掲示板を選ぶ」というルールのもとでは、決して砂糖は手に入らないのです。このような方策は決定論的（Deterministic）と呼ばれています。

　例えば将棋を考えてみましょう（図７）。蟻が決定論的な強化学習で将棋を学習したとします。このとき先手の（決定論的な）蟻は、いつも、はじめに、同じ手、例えば「２六歩」を指します。この勝負に蟻が勝ったとしても、次の対戦で蟻が先手の場合は、蟻は再び初めに「２六歩」を指し、さきほどの勝負とまったく同じ手を、次々に指してきます。

　これでは、さすがのキリギリスも何か対策をうってきますよね。なにせ相手の蟻は、なんと毎回同じ手を指してくるのですから。
　キリギリスからみると、最初は「蟻は強い！」と思っていたものの、何回も対戦すると次第に「何やってるの？」と疑いはじめてくるに違いありません。

図７

　これを避けるための方法が確率論的（Stochastic）な手法です。「一番大きな得点がかいてある掲示板」と「二番目に大きな得点がかいてある掲示板」（いずれも得点１以上）のどちらかを、確率的に（サイコロをふって）選ぶという方法です。この方法であれば、蟻もたまに砂糖を食べることができるようになります。

　対戦相手がいるような場合は確率論的な手法が重要になりますが、機械の制御などの場合は相手を欺く必要がありませんので、ベストな答え、すなわち決定論的な方法で十分ということになります。

３　選択数と次元の呪い　　―　離散量と連続量　―

　図６では、家や休憩所にいるときの蟻の選択肢の数は、わずか２個でした。例えば、休憩所S1に蟻がいるときの選択肢の数はS3、S4の２個です。このように、右か左か、１か２かなどは、離散量（discrete）と呼ばれています。Q学習（DQN)は選択肢が離散量のタイプです。

　ここで車の運転を考えてみます。ハンドルは右に180度、左に180度回転することができるとします。そして１度単位でコントロールしたい場合、その選択肢の数は360個にもなります。
　車にはアクセルとブレーキがついているので、選択肢の数はさらに膨らみます。アクセルを踏む角度を50分類、同じようにブレーキを踏む角度を50分類とすれば、結局　360×50×50　＝　900,000個の選択肢が、そこには並ぶことになります。900,000個の選択肢から一つを選ぶというのは理論的には可能だと思いますが、一つ隣を間違えて選ぶとだいぶ運転が変わってくるようなケースもあるので、やはり現実的ではないようです。

　そこで、Q値の学習と、次のポイントの選択（方策）を分けて考えよう、というアイデアがでてきました。図６ではQ値の値を基準に、どちらを選ぶかを決定しています。すなわち、「一番大きな得点（Q値）が書いてある掲示板を選ぶ」という方策でしたので、Q値の学習と、次のポイントの選択（方策）が一体となっています。
　これを、Q値を学習・推測するアルゴリズム（Critic）と、次のポイントを選ぶ（方策）というアルゴリズム（Actor）を分けて考えて、次のポイントを選ぶ（方策）というアルゴリズムでは、ハンドルの角度、アクセルの量、ブレーキの量にあたる「３種類の実数（連続量、continuous）」を専門に学習・予測させるようにします。
実数として考えると、わずか３種類の値を推測すればよいことになります。

　Q値の学習を行う部分はCritic、次を選択する方策はActorと呼ばれており、これらの２つがセットになったアルゴリズムはActor-Criticと呼ばれています。

４　Actor-Critic

　Actor-Critic 自体は、強化学習のアルゴリズムとして昔から提案・研究されていました。サーボモータを制御するためにロボット制御などでもよく使われた技術のようです。問題は、これとディープラーニングをどう融合させるかです。
　CriticはQ値を学習・推測する処理なので、DQN（Q学習）とほぼ同じアルゴリズムでOKですが、次のアクションを決定するActorのネットワークの重みをどのように更新していくか、が悩みどころでした。

　これについては、DeepMind社のSilver氏が2014年に、ニューラルネットワーク更新時の勾配を次のように計算すればよいことを示しました。
勾配がわかると、ネットワークの重みパラメータを更新することができます。

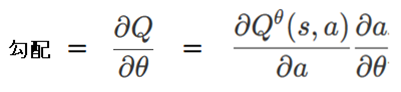
　目標は、Q値が最も大きくなるようなニューラルネットワークの重みパラメータθを求めることです。
　Q値が大きくなる方向に、ネットワークの重みパラメータθの値を少しずつ変動させたいのですが、その変動に使用する勾配（∂Q／∂θ）は、（∂Q／∂a） と（∂a／∂θ）の合成勾配として表わすことができることを示したのです。（aはアクション）
TensorFlowなどのディープラーニング用のフレームワークを利用すると、このような合成勾配を求めるプログラムも数行で実装できるので、とても便利です。

　ディープラーニングを使用したActor-Critic アルゴリズムは、その後DDPG（Deep Deterministic Policy Gradient）や、GPUを使用しなくても効率的に学習を進めることができるA3C（Asynchronous Advantage Actor-Critic）へと発展していきました。

５　報酬の与え方が決め手

　ディープラーニングを用いた強化学習は、今でも、そしてこれからも様々なモデルがでてくると思いますが、どのようなモデルであっても、どうやら決め手となるのは「どのように報酬を与えるのか」という点のようです。
　報酬の与え方が悪いと学習がまったく進まないことも多いようで、黒魔術的な要素がますます増えてきたように感じます。

次回は、このDDPGを使用した強化学習の事例（Part 2）をご紹介したいと思います。