こんにちは。 今回はベイジアンネットワークをテーマにしたいと思います。
最初にベイズ確率についてお話しします。
ベイズ統計「見えないものをさぐる ―それがベイズ」を出版しました。詳しくはこちらをご覧下さい。
画像認識と強化学習(DQN)を中心とした、ディープラーニングの書籍「実装 ディープラーニング」を、オーム社から出版しました。詳しくはこちらをご覧下さい。
ベイズ確率
ベイズの定理でよく例題にあげられるのが、病気の確率の問題です。
| <例題> ある病気を発見する検査法は、その病気の99%を発見するが、健康な人の3%にも反応し誤った診断を下すという。日本国内にはその病気の患者は0.1%であることがわかっている。 さて、ある日本人がこの検査を行なったら病気であると診断された。 この人が本当にその病気の患者である確率は何%か? |
病気である事象を B1、病気でない事象を B2、検査で病気と判定される事象を A とすると、例題は下図ように整理することができます。
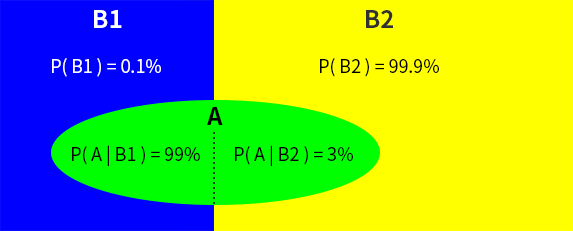
検査で病気と判定された(A)ときに、その病気である確率(B1)を求めるので、条件付き確率 P( B1 | A ) を求めればよいことがわかります。
ベイズの定理より、P( B1 | A ) = 0.0319 となり、例題の答えは、 3.2 % となります。
たとえ検査で陽性になったとしても、その病気である確率はわずか 3.2 %でしかありません。
この検査だけでは判断が難しいので、精密検査を受けた方がよさそうです。
さて、ここでポイントとなるのは、日本国内の話に限っているという点です。
もし検査を受けた人がフランス人であれば、実は確率は計算できません。
ベイズ確率は、事前確率・事後確率という考え方がベースにありますが、そのイメージは下図のとおりです。

「あるお寿司屋さんでよく売れるネタは、マグロ、タコ、エビであった。
さて、50歳代の女性が来店したが、この女性が最初に注文するネタはなんだろうか?」
考え方としては、過去の50歳代の女性のデータを集計すれば答えが見えてきますが、過去の50歳代の女性の来店がわずか2人であったとしたらどうすればいいでしょう?
単純に考えると、この2人がともに最初にタマゴを注文していたら、タマゴを注文する確率が100%になってしまいます。
このような時にベイズ確率を利用すると、このお寿司屋さん全体の状況を事前確率と考えることにより、そのお店に来店する50歳代の女性の確率を、常識的な範囲で推測することができます。
ベイジアンネットワーク
上記の例題の状況を、ベイジアンネットワーク(Bayesian network)上に表してみます。
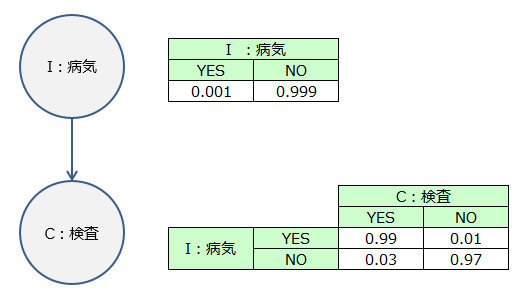
この関係を、ベイジアンネットワークをグラフィカルに表せるフリーソフトウェア Weka を利用して表してみます。I や C は「ノード」と呼ばれています。
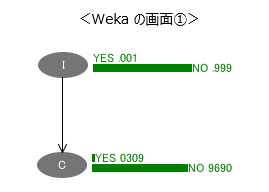
ノード C の「YES」が 0309 となっていますが、病気か病気でないか不明の状態でこの検査を受けると、3.09 % の人が陽性と判定されることを、ここでは示しています。
ここで、「ある日本人がこの検査を行なったら病気であると診断された」という事実、つまり エビデンスをノード C にセットすると、確率が再計算され以下のように表示が変わります。
エビデンスをセットした瞬間、ノード I は事前確率から、「ノード C = YES」という条件のもとでの、事後確率に変わります。
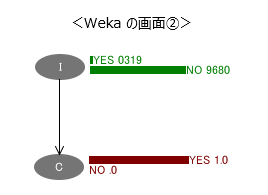
ノード I のYESの確率が事前確率 0.001 から事後確率 0.0319 に変わりました。
「ある日本人がこの検査を行なったら病気であると診断された」場合、病気である確率は 3.2 %であることがわかります。
このようにベイジアンネットワークは、ベイズ確率を基本としています。上記の例では2階層のベイジアンネットワークですが、3階層以上になると計算が複雑になりますので、 Weka などのツールを使った方が便利です。
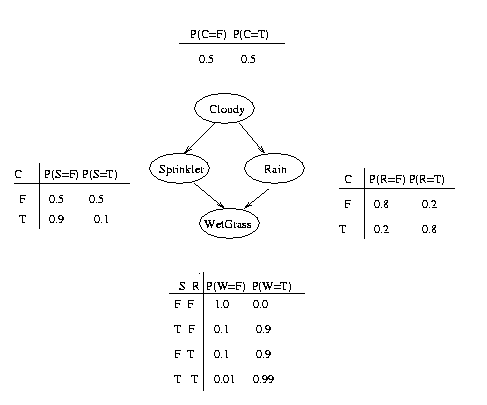
これは3階層のベイジアンネットワークの例ですが、「芝が濡れている」状態をエビデンスとすると、「曇っている」確率は約 58 % になります。
空を見なくても、芝の状態を見るだけで曇りかどうか推定できるということになります。
ベイジアンネットワークは、いろいろな事がらの因果関係をネットワークとして表現できますので、世の中にある複雑な因果関係を整理するのにとても役立ちそうです。
しかし因果関係がわかっていても、その確率自体がわからないと利用できません。
これにはある程度人の直感も必要になる場合がありますが、活躍するのはビッグデータの活用かもしれません。
